Spring 1997 AGU Meeting..... Poster SH51A-15

EVIDENCE FOR NONRADIAL SOLAR WIND ACCELERATION IN MAGNETOSTATIC CORONAL HOLES

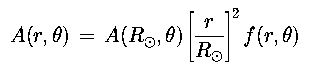
S. R. Cranmer (1), L. Strachan (1), M. Romoli (2), D. Dobrzycka (1), A. V. Panasyuk (1), and J. L. Kohl (1)

(1) Smithsonian Astrophysical Observatory, Cambridge, MA 02138, USA

(2) Universita di Firenze, I-50125 Firenze, Italy

ABSTRACT:

We compare UVCS/SOHO observations of densities and outflow velocities in polar coronal holes with theoretical mass-conservation models of an idealized force-free magnetostatic geometry. Open flux tubes bordering the closed-field streamer belt initially expand much more rapidly than flux tubes over the poles, then turn nearly radial and expand less rapidly. In the past, this variation in the superradial expansion factor has been inversely correlated with solar wind velocity at 1 AU, but we find an even stronger inverse correlation in the acceleration region of the solar wind (1 to 10 solar radii).

A considerable reduction in the wind speed of low-latitude flux tubes, compared with those over the poles, results in a geometry-dependent variation in the Doppler dimming of UV resonance lines such as H I Lyman alpha. Thus, we are able to use these emission diagnostics not only to infer the magnitude of the solar wind velocity, but also to map out the geometry of the solar wind emerging from large polar coronal holes.

This work is supported by NASA under Grant NAG5-3192 to the Smithsonian Astrophysical Observatory, by the Italian Space Agency, and by Swiss funding agencies.

(1) Observational Motivation:

• The Ultraviolet Coronagraph Spectrometer (UVCS), operating on board SOHO, observes the extended solar corona from 1.5 to 10 solar radii from sun center ( Kohl et al. 1995; Kohl et al. 1997; Kohl et al. 1998; see also the UVCS Home Page).

• UVCS primarily scans the solar corona in the Lyman alpha (H I 1216) and O VI 1032, 1037 spectral lines. We also measure electron density using polarized white light.

• In the large polar coronal holes seen around sunspot minimum, the electron density drops off rapidly with radius, but is constant in latitude (see, e.g., Guhathakurta and Holzer 1994).

• However, Lyman alpha intensity gradually rises with latitude (from pole to equator) in coronal holes, long before the high-density streamers are reached! Why?

• Scattered Lyman alpha intensity is a function of:
  1. neutral hydrogen density (which approximately scales with electron density)
  2. chromospheric Lyman alpha emission
  3. outflow wind velocity
  4. microscopic velocity distribution (i.e., unresolved thermal or nonthermal motions)

• Interaction between 2, 3, and 4 cause "Doppler dimming," which we find must vary with latitude in coronal holes.

(2) Magnetostatic Model:

• We apply the force-free analytic potential-field solutions of Low (1986), which are dipolar near the sun, and radial far from the sun. (See also Charbonneau and Hundhausen 1996.)

• One free parameter, the cusp radius, determines the inner radius of the equatorial current sheet. We choose a cusp radius equal to 5.5 solar radii, so that the coronal hole/streamer boundary occurs at a colatitude of 28 degrees from the pole (as observed with UVCS):

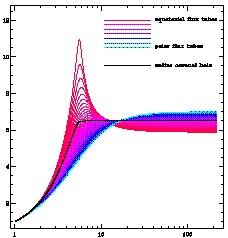
We use the same color code for flux tubes in most figures in this poster: BLUE tubes emerge from the poles, and RED tubes emerge from the edges of the coronal holes. The closed-field regions (ORANGE) do not enter into the following analysis of the solar wind.

(3) Magnetic Flux Tubes:

The cross-sectional area of individual flux tubes is determined by the assumed magnetostatic model. We define the nonradial expansion factor f in terms of the area A:

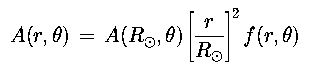
If f equals 1, the expansion is in the form of "radial cones." If f is greater than 1, the expansion is "superradial." (See Wang and Sheeley 1990, for models with similar expansion morphology.)

Here we plot f(r) for the flux tubes plotted above, as well as the expansion factor for the entire coronal hole taken as a single flux "bundle." The expansion is very superradial, with asymptotic values of f of 5 to 7:

(Click on Figure for full-size GIF)

Notice especially the differences between the flux tubes along the poles and those bordering the edge of the streamer belt. These differences are averaged out when only looking at the expansion factor of the total bundle of coronal-hole flux tubes (black line).

(4) Mass Flux Conservation:

Along each open flux tube, if we assume a time-steady flow, the equation of mass conservation gives:

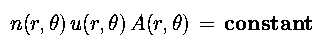
The number density n is measured by UVCS in white light. Its latitudinal dependence is consant in coronal holes, with a sharp rise in equatorial streamers. The observed geometry for coronal holes has been inferred from a set of "synoptic" measurements made in November 1996, and empirically modeled as follows:

(Click on Figure for full-size GIF)

The flux-tube area A is given by the assumed magnetostatic model geometry, and the constant in the mass flux conservation equation is given by measurements at 1 AU (see, e.g., Goldstein et al. 1996, or the Ulysses/NASA Home Page).

Thus, we can solve for the wind velocity u along each flux tube:

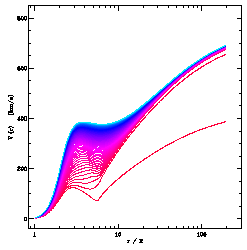(Click on Figure for full-size GIF)

Note that most flux tubes have the same "terminal" velocity at 1 AU (with the exception of those nearest the high-density streamer belt). However, the pole-to-equator variations are much more gradual at lower radii in the corona. These variations are what we hope to measure with UVCS using the diagnostic of Lyman alpha Doppler dimming.

(5) UVCS Observations:

To test the derived wind velocity field, we scan coronal holes along constant radii in Lyman alpha radiation, and plot the relative intensity increase (from pole to equator) versus colatitude theta.

In the following figures, we compare observations (points) with three models:

1. (Solid lines): Velocity vectors follow the flux tubes, and we use mass conservation for u as a function of radius and latitude. (This is the most self-consistent model.)

2. (Dashed lines): Velocity vectors follow the flux tubes, but we use only the polar magnitude of u at all latitudes. (In other words, we neglect the effect of varying f with latitude.)

3. (Dotted lines): Velocity vectors point radially, and we use the polar magnitude of u at all latitudes. (This spherically-symmetric case is the simplest model, but it is also the most unrealistic.)

Here we plot the comparisons at several heliocentric observing distances (1.5, 2.0, 2.5, 3.0, 3.5 solar radii):

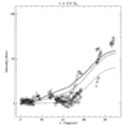
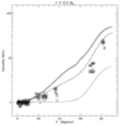
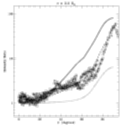
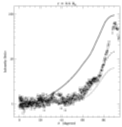(Click on Figures for full-size GIFs)

The model which seems to agree with most of the data points is the one with velocity vectors following the superradial flux tubes, but with no latitudinal variation in the velocity magnitude (dashed lines).

CONCLUSIONS:

• Doppler dimming of ultraviolet coronal lines can probe the geometry of the solar wind in addition to the magnitude of the outflow speed.

• The best fit between observations and models occurs when we assume...
  1. The direction of u(r) follows superradial stream lines in coronal holes,
  2. The magnitude of u(r) is constant in latitude.

• The simple magnetostatic force-free model, which results in strong latitudinal gradients in f(r), is thus probably not a valid description of the solar wind flow tubes.

These results lead us to postulate a general qualitative requirement for future models of the fast solar wind emerging from polar coronal holes: a valid model of the large-scale magnetic field must have f(r) be more "evenly distributed" from pole to equator, than the force-free model presented here.

REFERENCES:

(Links are to ADS abstracts and, where available, full online papers.)

Charbonneau, P., and Hundhausen, A. J. 1996, Solar Phys., 165, 237

Goldstein, B. E., et al. 1996, Astron. and Astrophys., 316, 296

Guhathakurta, M., and Holzer, T. E. 1994, ApJ, 426, 782

Kohl, J. L., et al. 1995, Solar Phys., 162, 313

Kohl, J. L., et al. 1997, Solar Phys., 175, 613

Kohl, J. L., et al. 1998, ApJ Letters, 501, L127

Low, B. C. 1986, ApJ, 310, 953

Strachan, L., Kohl, J. L., Weiser, H., Withbroe, G. L., and Munro, R. H. 1993, ApJ, 412, 410

Wang, Y.-M., and Sheeley, N. R., Jr. 1990, ApJ, 355, 726

Withbroe, G. L., Kohl, J. L., Weiser, H., and Munro, R. H. 1982, Space Sci. Rev., 33, 17