---

OVERVIEW

For this project, you can choose one of three options:

1. You can create and write up two new homework problems (with answer keys) of similar size and scope as the existing homework problems for this course. Please consider this option if I have not yet shown any examples or applications from the topical research area that you find most interesting!

2. You can choose a relevant paper (from a journal, or arXiv, or references that I give in the lecture notes) and review it with two written components: (a) a brief pedagogical summary, as if you were preparing lecture notes to teach it to a new class of Math Methods students, and (b) a mock referee's report, which includes criticism for the authors that is as specific and constructive as possible. Of course, the aspects that you focus on must be relevant to Math Methods.

3. You can choose a relevant paper (also relevant somehow to Math Methods, as above) and reproduce some of its key results. This is likely to involve some combination of writing code, re-deriving equations, downloading data, and/or making figures. Your write-up will present your versions of the results as well as your insights about how straightforwardly "reproducible" the original paper was.

In order to help you hit the ground running, in Homework 5 I'll ask you to start thinking about which option you want to pursue. In your submission, you'll include a brief written summary of what you'd like to do, what specific topic(s) you'll consider, and any other details you have at this time. If you want to do options (2) or (3) and you still haven't identified a specific paper, please feel free to describe the type of research that you'd like to investigate, and I can help you identify a paper. Also, if you want even more lead-time, please feel free to submit this information to me (say, by email) at any earlier time, and I'll do my best to provide feedback before the start of the two-week period that you'll be working on the project.

Lastly, I should note that you're not 100% locked into the ideas that you submit now. However, if you decide to change it after submitting, please let me know.

---

GRADING

We will use a 30-point scale for the grading, and then later re-scale it to be worth 15% of the final grade. Each option is graded on the basis of three equally-weighted categories:

1. New Homework Problems:
   • Problems clearly test knowledge of Math-Methods-relevant topics, and sufficient information is provided so students know what to do. (10 pts)
   • The answer key is understandable and useable for grading. (10 pts)
   • Problem and answer key both contain sufficient quantity of material (e.g., number of parts; difficulty level). (10 pts)

2. New Paper Review:
   • Pedagogical summary is clear, accurate, and pitched at an appropriate level for teaching in Math Methods. (10 pts)
   • Referee report is "specific, factual, and constructive." (10 pts)
   • Both parts contain sufficient quantity (e.g., summary covers 10-20 minutes of class; referee report isn't just about a small subset of the paper). (10 pts)

3. Reproduction of Results:
   • Written descriptions of the paper's content, the student's reproduction goals, and the results are clear and understandable. (10 pts)
   • Evaluative insights are provided about the original paper's comprehensibility and reproducibility. (10 pts)
   • Quantitative output (e.g., figures and other results) sufficiently conveys engagement with, and understanding of, the material. (10 pts)

For each category, the full 10 points corresponds to meeting all the criteria with no significant problems. 8 or 9 points corresponds to generally meeting the criteria, but with minor problem(s) that could have been handled better. 7 points or fewer corresponds to clearly not meeting some aspect of the listed criteria.

---

EXAMPLE TOPICS:

First, a few general thoughts:

• The original guidelines talk a lot about finding published papers to analyze. However, the paper doesn't have to be the first thing that you find. It's okay to start with an interesting concept from anywhere, then search the internet for additional information (in order to figure out if the "math methods" involved are of the right scope for this course), and then find the relevant journal paper(s) after that.

• This project is an opportunity for you to explore something new and different, so I'll discourage you (but not outright forbid you) from exploring a topic in your own research sub-field. In any case, please don't reuse/rebrand a pre-existing code or analysis tool from a research project of yours.

Next, the actual list. You're not limited to these topics, of course. If you do choose something from this list, please try to customize it (i.e., "make it your own") in some way...

• Paging through the archives of the Astronomy Picture of the Day yields an abundance of visual wonders that can be simulated with the mathematical tools of this course! For example, you could build a model of the solar analemma (or maybe its lunar analogue). You could simulate a rainbow with all of its multiple-scattering orders (primary, secondary, tertiary, etc). You could explore the equations that distinguish synchrones from syndynes in cometary tails. Many more examples can be found.

• We examined a number of numerical root-finding methods, with some that converge quite rapidly. Astronomers in 2022 found a method that's faster than most of them (when applied to gravitational microlensing problems, at least). Might Aberth-Ehrlich replace Newton-Raphson in the textbooks?

• When stars or planets are orbiting one another in very close proximity, there are tidal forces that distort their shapes away from exact spheres. Can you develop ways to compute (and understand conceptually!) the shapes of these Roche lobes for observers at various orientations? Can one go further and compute how these shapes are modified when other forces are present, or if gravity itself is modified?

• Do you need to find the largest eigenvalue of a huge matrix? The folks at Google PageRank do, and they apply a variant of a deceptively simple-looking method called power iteration. Does it always work as intended? How much faster is it than computing those eigenvalues the usual way?

• We talked about "ordinary" least-squares methods in lecture set 2, but there's a generalization (total least squares) that takes into account uncertainties in both the x and y values (see tweet below). Are there situations that essentially demand we use one method or the other?
  

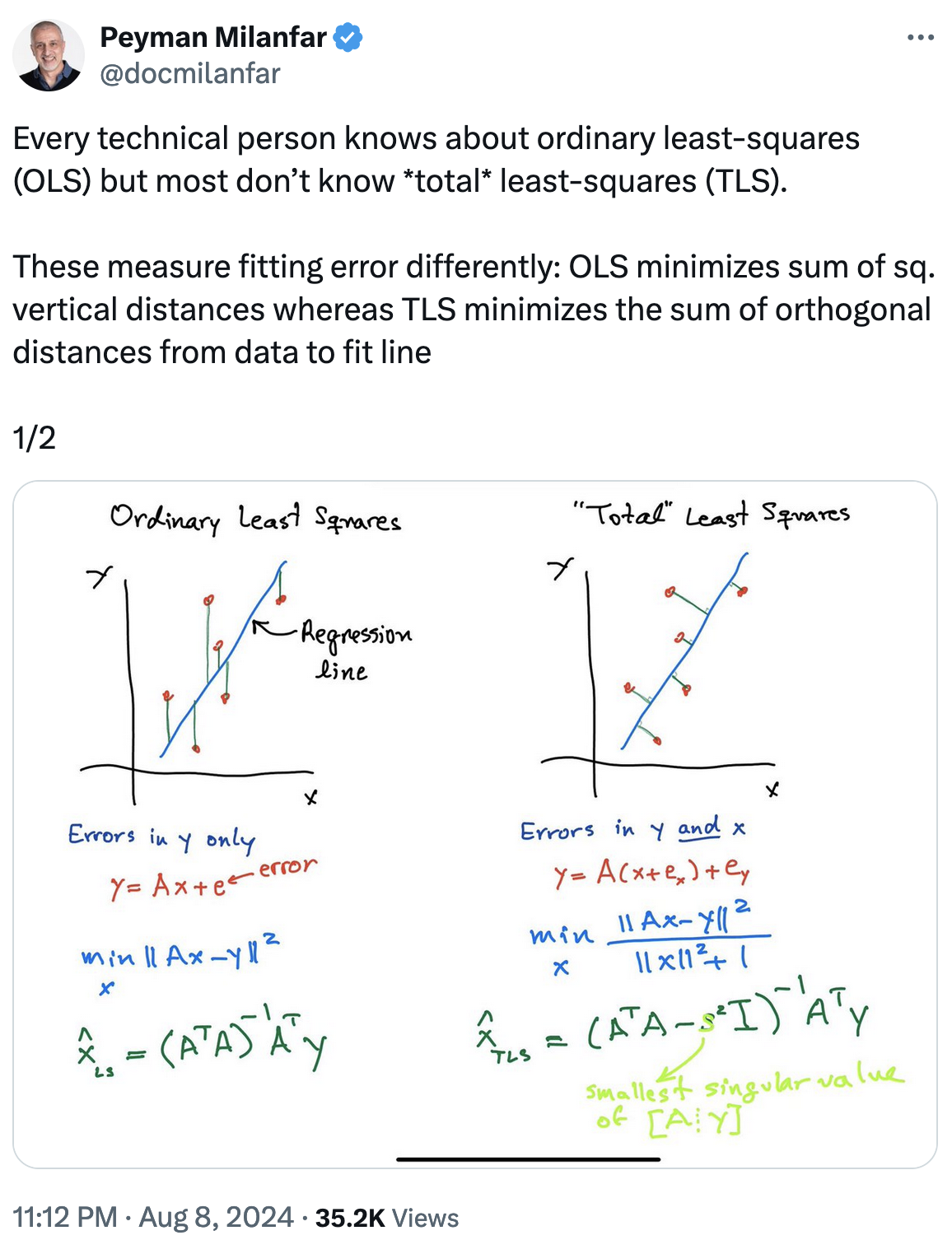
• You can use orthogonal transformations (e.g., Euler and other matrices) given in lecture set 2(d) to write your own CGI "rendering" code. In other words, if you specify the 3D positions of various objects, can you show how an observer would see them (projected on a 2D "viewscreen") at various finite distances and orientations? Can one use such a code to assess the accuracy of the various perspective techniques developed by Renaissance painters?

• In class, I noted a nice Picture of the Day about "Chicagohenge." What about Boulder? Could this ever happen along Pearl Street (or choose your favorite street)? There's some math involved with computing the dates and times when alignments like this may occur. However, what's true today may not be true in the past or future. The Earth's obliquity and precession axis -- as well as the eccentricity and inclination of our orbit around the Sun -- vary over timescales of thousands to millions of years. Thus, there's probably some numerical ODE-solving that would need to be done in order to predict how far into the past and/or future a given street-alignment would persist!

• Almost 70 years ago, there was an interesting astronomical application of method of undetermined coefficients for solving an inhomogeneous ODE. Contopoulos (1956) used it to find the equations of motion for stars in an elliptical galaxy. A strange feature of that paper (which maybe wasn't that strange, then) was that it has no figures. Thus, I think it's a great candidate for a "reproduce these results" project... as long as you show us how a modern-day scientist would highlight these interesting results with equally-interesting plots and/or images!

• In lecture set 4 (d.3), I introduced North's (1975) energy-balance model of the Earth's climate. In that model, we ignored both diurnal (day/night) and annual (seasonal) time-variability. If you put those back in, you will have turned the ODE into a PDE. With this, you can determine why the hottest part of the day is usually a few hours after noon, and why the hottest part of the year is a few months after the summer solstice. It's also possible to put in longer-term variability, from, say, anthropogenic CO₂. How much does one have to vary the parameters of these models before the Earth turns into either a frozen ice-ball, or a runaway hot-house?

• If you're also taking AMP (ASTR-5110), you will have seen many different ways that the Schrödinger equation is relevant to physics and astronomy. Why not apply the many ODE and PDE techniques that you're learning here to find useful solutions to the Schrödinger equation for, e.g., traveling particles, particles trapped in potential wells, particles encountering potential barriers, and so on? The sky is the limit! (Well, ℏ is really the limit...)

• We have examined examples of the diffraction of light around solid obstacles in several places (e.g., lecture set 3 (c.5), and lecture set 4 (d.3)). In real telescopes, though, the shapes of the open apertures aren't simple circles or rectangles. Telescopes often have central mirrors (which make for donut shaped apertures) or "spider-leg" struts that block out even more of the apertures. Linear ("knife-edge") occulters are sometimes replaced by "serrated" (sawtoothy) occulters. Can you compute the diffraction patterns generated by these complications, and thus investigate ways of minimizing the spread of diffracted light?

      On a related note, can you simulate the spot of Arago?

• Lastly, here's an example PDE project idea from Brad Hindman, that may help you prep for ASTR-5400 (Fluids):
  

---

---